Continuiamo a parlare della teoria relativa alla costruzione del Portafoglio.
Rischio e rendimento
Mentre il termine rendimento ha un chiaro significato ovvero l’apprezzamento (o il deprezzamento) nel tempo di un investimento la parola rischio può corrispondere a vari aspetti, in questo articolo ci concentreremo sul rischio come volatilità (ovvero varianza dei rendimenti).
Ogni giorno valutiamo i rischi rapportato alla utilità di una scelta. Non solo scelte di carattere finanziario ma anche di carattere personale. In finanza il rapporto tra Rischio e Rendimento è la base per la valutazione e/o la scelta un investimento.
Come passare però dalla teoria a dei numeri concreti per procedere con le nostre analisi e costruzione di portafoglio ?
Gli investitori possono usare l’analisi della media / varianza per prendere decisioni su quali strumenti finanziari investire, in base a quanti rischi sono disposti ad assumersi in cambio di diversi livelli di rendimento.
Inserisci il tuo indirizzo e-mail e riceverai le notifiche per i nuovi articoli :
Rendimento -> Media
Il rendimento considerato per le analisi viene anche chiamato media, poiché ci riferiamo al valore atteso (media, expected value in inglese). A seconda dei casi casi può essere il rendimento storico o un rendimento prospettico (annuale/mensile etc..) che ci si aspetta di ottenere dato un certo orizzonte di tempo.
Rischio -> Varianza
Nella teoria della probabilità, la varianza è il quadrato della deviazione standard di una variabile dalla sua media. Viene utilizzata per sintetizzare il rischio di un investimento e spesso si usa anche il termine volatilità.
Possiamo dire che a livello lessicale (e non statistico) le parole volatilità/rischio/varianza/deviazione standard vengono spesso usate come sinonimi.
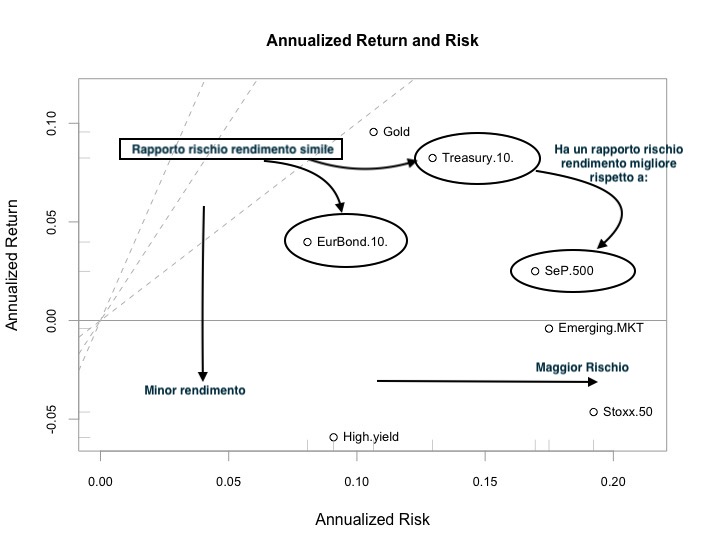
Analizzando la figura d’esempio in alto vediamo come EuroBond abbia una volatilità e un rendimento migliore di S&P500 e sia da preferire. Ma tra Treasury e EuroBond? Paghiamo un maggior rendimento a fronte di una maggior volatilità. A questo punto la scelta va fatta considerando la nostra propensione al rischio e i nostri obiettivi.
Se però volessimo un portafoglio che centri i nostri obiettivi ? Un ipotetico investimento con caratteristiche comprese tra quelle di Treasury e EuroBond? Come passiamo dal rendimento e rischio di un asset a quello di un portafoglio?
Ipotizziamo di costruire un portafoglio composto da 2 investimenti nel quale :
- L’investimento A abbia un rendimento Ra e una deviazione standard Da
- L’investimento B abbia un rendimento Rb e una deviazione standard Db
- La correlazione tra A e B sia pari a C
- Il peso % nel portafoglio di A sia Pa
- Il peso % nel portafoglio di B sia Pb
Possiamo costruire un portafoglio con le caratteristiche da noi desiderate in termini di rischio o di rendimento variando i pesi Pa e Pb.
Rendimento del portafoglio = (Pa* Ra) + (Pb* Rb)
Vediamo come il rendimento del portafoglio sia semplicemente la media dei rendimenti dei componenti.
Il rischio di portafoglio
Varianza (Rischio) di Portafoglio = (Pa2 * Da2 ) + (Pb2 * Db2 ) + (2*Pa*Pb*Da*Db*C )
Vediamo come il rischio di portafoglio sia caratterizzato dal un terzo termine in cui abbiamo un prodotto tra le deviazioni standard dei componenti, i loro pesi e la loro correlazione. Possiamo notare che se C = 0 il terzo termine si annulla e se C < 0 ovvero se la correlazione tra i due componenti è negativa il terzo termine diventa negativo e sottragga volatilità al portafoglio.
Capiamo quindi l’importanza di componenti debolmente o negativamente correlati nella costruzione dei portafogli di investimento. Questa caratteristica infatti non vale solo per portafogli con 2 componenti ma, con formule più complesse, anche da n componenti.
assetallocation Bitcoin Certificati Cina Correlazioni Covid Crypto ESG ETF FactorInvesting Investimenti Megatrend obbligazioni Oro Pensioni PIR Portafogli REIT Risk Teoria di Portafoglio Volatilità

11 pensieri su “Teoria di Portafoglio II – Rischio e Rendimento”