Oggigiorno il conoscere e il modellizzare il comportamento di determinati asset è diventato sempre più importante non solo per esigenze di trading, ma anche per esigenze normative. La gestione del rischio e la gestione di portafogli si basano sempre più sui valori di media e varianza. Alla base di questi modelli abbiamo la distribuzione dei rendimenti di un determinato asset.
Vedrò in questo articolo di introdurre a questi concetti nel modo più semplice possibile.
Dato un insieme di prezzi possiamo calcolare i rendimenti (anche detti ritorni) ovvero le variazioni dei prezzi su base oraria, base giornaliera, settimanale, mensile o annuale. Dalle serie storiche sono ricavati i rendimenti , in maniera discreta o in caso di incrementi non superiori al 30% con l’approssimazione del logaritmo naturale. Generalmente si osservano le distribuzione dei rendimenti giornaliere e mensili. Una volta calcolati questi rendimenti possiamo osservare ad esempio quante volte abbiamo avuto un ritorno maggiore del 5%, quante volte tra il 4 e il 4.9% e così via. In questo articolo utilizzerò i rendimenti giornalieri, settimanali e mensili del titolo Apple.
La distribuzione dei rendimenti
In statistica, una distribuzione è una rappresentazione del modo in cui le diverse modalità di un carattere si distribuiscono nelle unità statistiche che compongono il collettivo oggetto di studio.
In finanza si è soliti analizzare e tenere in considerazione la distribuzione dei rendimenti di un determinato asset, ovvero un indice, una azione o un’obbligazione.
Istogrammi
Una soluzione per visualizzare la distribuzione dei rendimenti è quella di utilizzare un istogramma nel quale vengono indicate sull’asse delle ascisse i valori dei rendimenti e su quella delle ordinate la frequenza in con la quale sono presenti nei dati storici.
Vediamo prima un banale esempio didattico, un istogramma in cui abbiamo 4 osservazioni, 1 tra -1% e 0, 2 tra lo 0 e il +1% e infine 1 tra 1% e 2%.
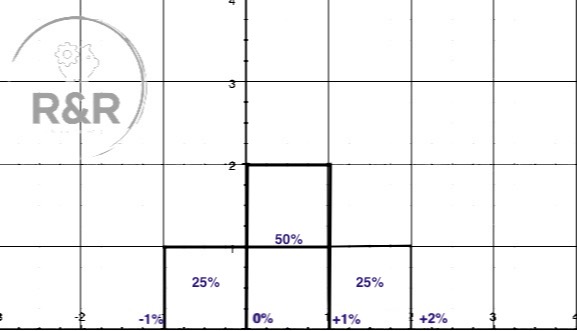
Possiamo in questo caso dire che, se i rendimenti futuri si basassero solo sui rendimenti passati, abbiamo un 75% di avere un ritorno positivo e un 25% di avere un rendimento maggiore del 1%.
Passiamo ora ai rendimenti giornalieri del titolo APPLE.
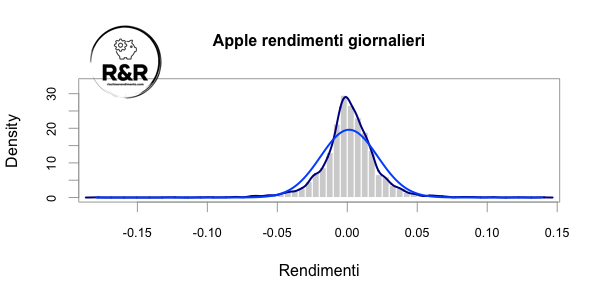
Come vediamo la maggior parte dei rendimenti giornalieri si concentrano vicino allo 0 e sono principalmente compresi tra +/-5%(0.05). In azzurro viene disegnata sull’istogramma una curva pari alla distribuzione normale.
La distribuzione Normale
La distribuzione Normale (o gaussiana), è una distribuzione di probabilità continua usata per descrivere variabili casuali a valori reali che tendono a concentrarsi attorno a un singolo valor medio, (la media μ) è simmetrica e varianza σ2. In un mondo senza accesso alla potenza degli elaboratori l’utilizzo della distribuzione gaussiana permette di calcolare attraverso la formula la probabilità di un rendimento di eccedere un certo livello x. Su molti libri di statistica sono presenti tavole con i valori della distribuzione normale al fine di semplificare i calcoli.
Nel 1900 Louis Bachelier presentò una tesi di laurea intitolata Teoria della speculazione introducendo per la prima volta la matematica e l’analisi probabilistica nel mondo della finanza. Questa tesi fu la base di più di 65 anni di studi sulla probabilità , sulle analisi stocastiche e dei lavori di Osborne (1959), Samuelson (1960) e Fama (1964) per modellizzare le variazioni di prezzo di commodities e azioni considerando determinati intervalli di tempo. Bachelier sostenne che le piccole fluttuazioni nei prezzi delle azioni fossero indipendenti dal valore delle azioni in quel momento e che fossero indipendenti e normalmente distribuite.
Se osserviamo il grafico vediamo un’altra linea di colore blu scuro che altro non è che una distribuzione dei rendimenti calcolata dal software per essere maggiormente simile ai dati. Torneremo dopo sull’importanza di queste modellizzazioni.
Differenze nelle distribuzioni su intervalli di tempo
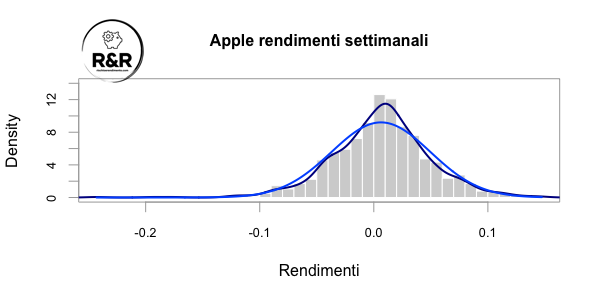
Se osserviamo il grafico dei rendimenti settimanali (da venerdì a venerdì) e quelli mensili, notiamo che la linea blu scuro si avvicina alla linea della normale, potremmo dire quindi che i rendimenti settimanali e mensili tendono ( in questo caso) a essere più normali di quelli giornalieri.

Inserisci il tuo indirizzo e-mail e riceverai le notifiche per i nuovi articoli (di solito 1-2 a settimana)
Boxplot
Oltre che gli gli istogrammi possiamo usare anche dei boxplot per rappresentare graficamente le variabili quantitative:
- istogramma: aiuta a capire dove si trova il punto centrale di una variabile e quanta variabilità c’è nei dati
- boxplot: aiuta a capire se la distribuzione è simmetrica e per confrontare la forma di più distribuzioni
Il Var – Value at Risk
Uno degli utilizzi della distribuzione dei rendimenti è il Value at Risk (VaR). I regolatori richiedono che una società finanziaria riservi del capitale per assicurarsi da eventi estremi di perdite sui portafogli. Il rischio di portafoglio è misurato in termini di Value at Risk e per esempio uno dei primi sistemi di controllo del rischio RiskMetrics (creato nel in 1989) si basava sulla sulla assunzione che i ritorni del mercato siano distribuiti normalmente.
Come abbiamo visto una volta calcolati i nostri rendimenti sulla base dei dati storici possiamo desumere (inferire) una distribuzione dei rendimenti valida per le nostre valutazioni sul rischio. Ipotizzando ad esempio che i rendimenti mensili siano distribuiti normalmente, possiamo calcolare il nostro VaR (generalmente si usa il valore del 95%).
Cosa si intende per VaR al 95% ? Si intende che il 95% delle volte (dei mesi in questo caso) il rendimento dell’asset sia maggiore di un certo valore. Nel grafico sottostante possiamo vedere come il valore di VaR al 95% sia circa -0.11 ovvero che il 95% dei mesi (19 mesi su 20) il titolo Apple non dovrebbe perdere più del 11%. Se osserviamo il grafico vediamo un secondo valore di VaR calcolato utilizzando la distribuzione calcolata dal software, un valore leggermente più basso.
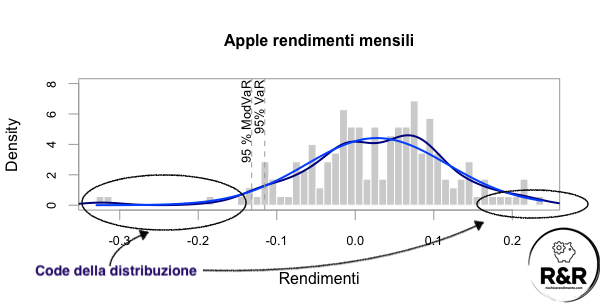
Come possiamo notare nella coda sinistra abbiamo alcuni valori molto negativi che il modello stima avere una probabilità molto bassa di accadere, mentre in realtà sono presenti con maggior frequenza. Riguardo a ciò nel libro il cigno nero Nassim Nicholas Taleb ritiene che si sottovalutino :
- il ruolo di eventi rari che sono oltre le reali aspettative nell’ambito storico scientifico e finanziario,
- la non computabilità della probabilità di eventi rari con metodi scientifici,
- il bias psicologico che rende cieche le persone rispetto a eventi rari.
Taleb propone anche l’utilizzo in finanza di distribuzioni a code ampie ( fat tail ) ovvero che considerino maggiormente la probabilità di eventi estremi rispetto alla distribuzione Normale.
In conclusione i prezzi e in seguito i rendimenti sono alla base per creare dei modelli che permettano di prevedere l’andamento probabilistico di un determinato asset nel tempo. Questi modelli sono poi utilizzati per la creazione di portafogli, per il controllo del rischio o per stimare il valore di derivati quali le opzioni.
assetallocation Bitcoin Certificati Cina Correlazioni Covid Crypto ESG ETF FactorInvesting Investimenti Megatrend obbligazioni Oro Pensioni PIR Portafogli REIT Risk Teoria di Portafoglio Volatilità

16 pensieri su “La distribuzione dei rendimenti e il VaR”